Bazén
Pokud do bazénu přitéká voda současně dvěma přívody, naplní se celý za 19 hodin. Jedním přívodem se naplní o 6 hodin později než druhým. Za jak dlouho se naplní bazén jednotlivými přívody zvlášť?
Správná odpověď:

Zobrazuji 2 komentáře:
Žák
v prvních dvou řádcích počítáte t1, ale kvadratická rovnice je jako by se počítalo t2. Pokud to spočtu tak jak je to zadáno, tak mi vyjde jiná kvadr. rov, a výsledek bude t1 = 28,88 a t2 je o těch 7h více.
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem harmonického průměru?
Hledáte statistickou kalkulačku?
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Chcete proměnit jednotky času, např. hodiny na minuty?
Hledáte statistickou kalkulačku?
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Chcete proměnit jednotky času, např. hodiny na minuty?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- statistika
- harmonický průměr
- algebra
- kvadratická rovnice
- rovnice
- soustava rovnic
- aritmetika
- odmocnina
- druhá mocnina
- umocňování
- základní funkce
- úvaha
- nepřímá úměra
- přímá úměra
- čísla
- zlomky
- reálná čísla
Jednotky fyzikálních veličin:
Téma:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Archimedes - vor
 Chci postavit vor, mám trámy o čtvercovém průřezu se stranou a=20cm a délce l=2m, hustota dřeva 670 kg/m³, spojím 10 trámů-jaký je objem voru a jeho hmotnost? Do jaké hloubky se vor potopí na vodě ( hustota vody 1000kg/m³ )? Hmotnost jednoho člověka je 50
Chci postavit vor, mám trámy o čtvercovém průřezu se stranou a=20cm a délce l=2m, hustota dřeva 670 kg/m³, spojím 10 trámů-jaký je objem voru a jeho hmotnost? Do jaké hloubky se vor potopí na vodě ( hustota vody 1000kg/m³ )? Hmotnost jednoho člověka je 50 - Vztlaková sila 3
 Kulaté ocelové závaží (ρ1=7800 kg/m3) je zavěšeno na vlákně a ponořeno do vody (ρ2=1000 kg/m3). Objem závaží je 1dm³. Jakou silou je vlákno napínané?
Kulaté ocelové závaží (ρ1=7800 kg/m3) je zavěšeno na vlákně a ponořeno do vody (ρ2=1000 kg/m3). Objem závaží je 1dm³. Jakou silou je vlákno napínané? - Vztlaková sila
 Betonový sloup o hustotě 3500kg/m3, ve výšce 6m a čtvercové podstavě a=25 cm leží na dně přehrady v hloubce 10m. Na horním konci je za lano zvedán jeřábem. 1) jak velkou silou napíná sloup lano, pokud je celý sloup ponořený ve vodě? 2) jak velk
Betonový sloup o hustotě 3500kg/m3, ve výšce 6m a čtvercové podstavě a=25 cm leží na dně přehrady v hloubce 10m. Na horním konci je za lano zvedán jeřábem. 1) jak velkou silou napíná sloup lano, pokud je celý sloup ponořený ve vodě? 2) jak velk - Povrch 32
 Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
- Do rovnostranného 2
 Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule?
Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule? - Podstavy
 Podstavami pravidelného komolého čtyřbokého jehlanu jsou čtverce. Délky stran se liší o 6 dm. Tělesová výška je 7 dm. Objem tělesa je 1813 dm³. Vypočítejte délky hran obou podstav.
Podstavami pravidelného komolého čtyřbokého jehlanu jsou čtverce. Délky stran se liší o 6 dm. Tělesová výška je 7 dm. Objem tělesa je 1813 dm³. Vypočítejte délky hran obou podstav. - Na rovnici paraboly
 V tenisovém zápase je Adrien 5 m od sítě, když odpálí míč vysoký 80 cm od země. Maximální výška jeho parabolické dráhy procházející přes síť byla 1,5 m . Pokud je délka kurtu je 23,77 m, dopadne míček dovnitř kurtu?
V tenisovém zápase je Adrien 5 m od sítě, když odpálí míč vysoký 80 cm od země. Maximální výška jeho parabolické dráhy procházející přes síť byla 1,5 m . Pokud je délka kurtu je 23,77 m, dopadne míček dovnitř kurtu? - Pro rozměry
 Pro rozměry plaveckého bazénu platí: d : š : h = 10 : 4 : 1. Do bazénu se vejde 625 m³ vody. Vypočítejte, kolik m² obkladů je třeba zakoupit na obložení stěn bazénu, přidáme-li 5% na odpad.
Pro rozměry plaveckého bazénu platí: d : š : h = 10 : 4 : 1. Do bazénu se vejde 625 m³ vody. Vypočítejte, kolik m² obkladů je třeba zakoupit na obložení stěn bazénu, přidáme-li 5% na odpad. - Pravoúhlého 75144
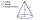 Poloměr pravoúhlého kruhového kužele je 9 cm a délka strany je 15 cm. Najděte na jedno desetinné místo: (i) Výši (ii) Objem kužele
Poloměr pravoúhlého kruhového kužele je 9 cm a délka strany je 15 cm. Najděte na jedno desetinné místo: (i) Výši (ii) Objem kužele
- V=4x^3+43x^2+63x 72764
 Největší vnitřní akvárium na světě. Ve své obrovské nádrži s kapacitou reprezentovanou následujícím polynomem V=4x³+43x²+63x Akvárium má tvar obdélníkového hranolu. Najděte následující: 1. Je-li výška akvária x, najděte plochu základny (B). 2. Na základě
Největší vnitřní akvárium na světě. Ve své obrovské nádrži s kapacitou reprezentovanou následujícím polynomem V=4x³+43x²+63x Akvárium má tvar obdélníkového hranolu. Najděte následující: 1. Je-li výška akvária x, najděte plochu základny (B). 2. Na základě - Zlatý 3
 Zlatý prstýnek o šířce 1 cm je vyroben provrtáním koule o poloměru 1 cm přes její střed. Zlatý náramek o šířce 1 cm je vyroben provrtáním koule o poloměru 4 cm přes její střed. Který šperk bude mít větší cenu pokud budeme brát do úvahy pouze množství drah
Zlatý prstýnek o šířce 1 cm je vyroben provrtáním koule o poloměru 1 cm přes její střed. Zlatý náramek o šířce 1 cm je vyroben provrtáním koule o poloměru 4 cm přes její střed. Který šperk bude mít větší cenu pokud budeme brát do úvahy pouze množství drah - Seříznutého 70434
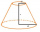 Vyjádřete povrch a objem seříznutého kužele pomocí jeho strany s, pokud pro poloměry postav r1 a r2 platí: r1 > r2, r2 = s a pokud odchylka strany od roviny podstavy je 60°.
Vyjádřete povrch a objem seříznutého kužele pomocí jeho strany s, pokud pro poloměry postav r1 a r2 platí: r1 > r2, r2 = s a pokud odchylka strany od roviny podstavy je 60°. - V jakém
 V jakém poměru je třeba smíchat roztoky koncentrace 82% a 54%, abychom získali 76% roztok?
V jakém poměru je třeba smíchat roztoky koncentrace 82% a 54%, abychom získali 76% roztok? - Vypočítejte 70294
 Délky hran čtyřbokého hranolu jsou v poměru a: b:c = 2:4:5. Povrch hranolu je 57 cm². Vypočítejte objem.
Délky hran čtyřbokého hranolu jsou v poměru a: b:c = 2:4:5. Povrch hranolu je 57 cm². Vypočítejte objem.
- Vypolévám 69154
 Určete výkon čerpadla pokud: Vypolévám s hadicí 3 m³ vody z nádrže za 120 sekund. Výška ústí hadice nad nádrží je 1,5m. Rychlost vody z ústí hadice je 20 m/s.
Určete výkon čerpadla pokud: Vypolévám s hadicí 3 m³ vody z nádrže za 120 sekund. Výška ústí hadice nad nádrží je 1,5m. Rychlost vody z ústí hadice je 20 m/s. - Spořit dnes
 Kolik musím měsíčně spořit, abych za 5 let naspořil 100 000 Kč, je-li úroková míra 4 %, úrokovací období jeden měsíc a daň z úroků 15 %?
Kolik musím měsíčně spořit, abych za 5 let naspořil 100 000 Kč, je-li úroková míra 4 %, úrokovací období jeden měsíc a daň z úroků 15 %? - Rychlostí 65984
 Kámen byl vržen svisle vzhůru rychlostí vo= 15m. s-1. Za jakou dobu bude ve výšce a) 10 m, b) 12 m?
Kámen byl vržen svisle vzhůru rychlostí vo= 15m. s-1. Za jakou dobu bude ve výšce a) 10 m, b) 12 m?
