Math word problems
Mathematical word problems allow you to practice your mathematics knowledge in everyday tasks. Word problems train to understand, translate into the mathematical language (e.g., equations), solve, and check the accuracy and solution discussion.
Choose a topic you want to calculate and improve in.
Choose a topic you want to calculate and improve in.
1025surface area
758cuboid
556cube
550prism
481cylinder
262pyramid
245cone
230sphere
56frustum
4794equation
434divisibility
304sets
502probability
313variations
260permutations
727mean
36variance
2249multiplication
1913division
1615subtraction
1536addition
1348square root
596comparing
551rounding
204cube root
168third power
3242length
3235time
3135area
2606unit conversion
2509volume
2072money
1524mass
1257angle
1119velocity
603power
399density
305temperature
254acceleration
196energy
326sine
307tangent
292cosine
62arcsine
2971square
2574area of a shape
2496triangle
1716right triangle
1004perimeter
990circle
969rectangle
543diagonal
288trapezoid
225polygon
199rhombus
79chord
50annulus
48rhomboid
22parabola
themes, topics
843work
172map scale
107Ohm's law
571line
178line segment
126vector
2206percentages
2149reason
1629ratio
246functions
179maximum
138factorial
107minimum
89per mil
25modulo
10integral
3163fractions
1816natural numbers
341integers
161real numbers
41matrix
From our database of math word problems and examples, we offer the following:
- Contains 5683
Livia, Pavla, and Samuel collect knives. Pavla has more of them than Livia and Samuel combined. Livia only contains blades for a short time, so she only has 5 of them, which is the least. He has a total of 25. How many knives does Samuel have? - A 500-gram
A 500-gram pack of delicious hotdogs costs P119.95. How many packs can be bought with P1000? - The missing digit
Complete the missing digit in the number 3 ∗ 43 to form a number divisible by three. If there are multiple options, list them all. (The omitted digit is marked with the symbol ∗. ) Answers must be justified! - Probability 83133
The mobile PIN has 4 characters. What is the probability that the PIN contains the number 7 and ends with the number 5? - Slope
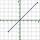What is the slope of a line with an inclination -325°? - The tank
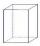The tank has 1320 liters of water and is shaped like a prism. Its base is a rectangle with sides a = 0.6 m and b = 1.5 m. How high is the water level in the tank? - Calculate 3561
There is a 12 cm long chord in a circle with a radius of 10 cm. Calculate the distance of the chord from the center of the circle. - Calculating 63344
Calculate the volume of the cone formed by rotating an isosceles triangle about the height of the base. The triangle has a side length of 15 cm and a height to the base of 12 cm. When calculating, use the value pi = 3.14 and round the result to one decima - Combinations 16283
How many elements is it possible to form twice as many second-class combinations as a fourth-class combination? - Perpendicular 3482
The lengths of the base legs are 7.2 cm and 4.7 cm, and the height of the prism is 24 cm. Calculate the volume and surface of a triangular perpendicular prism with the base of a right triangle. - Smaller 81015
Divide the area S=153 m² of the square garden in a ratio of 2:7. What part of the garden does the smaller part occupy? - Ted spent
Ted spent $20.75 on lunch and $56.23 on gas. If he started with $100, how much does he have now? - View angle - river
The 15 m high building is 30 m away from the river bank. The river's width can be seen from the roof of this building at an angle of 15°. How wide is the river? - Observatories A,B
The target C is observed from two artillery observatories, A and B, 296 m apart. At the same time, angle BAC = 52°42" and angle ABC = 44°56". Calculate the distance of the target C from observatory A. - Tent
A pyramid-shaped tent has a base square with a side length of 2 m and a height of 1.7 m. How many meters of canvas is needed to make it if we should add 10% for waste? - Kids
How many different ways can sit 6 boys and 3 girls in line if girls want to sit on the edge? - Equilateral cylinder
The equilateral cylinder (height = base diameter; h = 2r) has a V = 178 cm³ volume. Calculate the surface area of the cylinder.
more math problems »
