Math word problems
Mathematical word problems allow you to practice your mathematical knowledge through everyday situations. They train you to understand a problem, translate it into mathematical language (e.g., equations), solve it, and verify the accuracy of the solution.
Choose a topic you want to calculate and improve.
Choose a topic you want to calculate and improve.
1029surface area
758cuboid
556cube
552prism
483cylinder
262pyramid
246cone
231sphere
56frustum
4808equation
435divisibility
306sets
506probability
314variations
262permutations
729mean
37variance
2260multiplication
1919division
1623subtraction
1551addition
1374square root
598comparing
555rounding
204cube root
168third power
3254time
3251length
3149area
2624unit conversion
2516volume
2087money
1534mass
1262angle
1125velocity
604power
400density
308temperature
254acceleration
197energy
327sine
307tangent
293cosine
62arcsine
2992square
2603area of a shape
2501triangle
1720right triangle
1005perimeter
992circle
973rectangle
545diagonal
291trapezoid
226polygon
201rhombus
79chord
50annulus
48rhomboid
22parabola
themes, topics
845work
173map scale
107Ohm's law
573line
178line segment
127vector
2216percentages
2157reason
1636ratio
247functions
180maximum
138factorial
107minimum
100logarithm
89per mil
25modulo
10integral
3125fractions
1824natural numbers
343integers
162real numbers
41matrix
From our database of math word problems and examples, we offer the following:
- Theater
 Each row of the theater has 15 seats. The ticket to the first 7 rows is for 26 EUR. The next row is for 13 EUR. The theater was completely sold out. Revenue was 5850 EUR. How many rows are in the theater?
Each row of the theater has 15 seats. The ticket to the first 7 rows is for 26 EUR. The next row is for 13 EUR. The theater was completely sold out. Revenue was 5850 EUR. How many rows are in the theater? - Riley
 Riley has 4 mixing bowls. Each bowl has 1 5/8 cups of flour. How many cups of flour does Riley have? Show your work.
Riley has 4 mixing bowls. Each bowl has 1 5/8 cups of flour. How many cups of flour does Riley have? Show your work. - Parametric form
 Calculate the distance of point A [2,1] from the line p: X = -1 + 3 t Y = 5-4 t Line p has a parametric form of the line equation.
Calculate the distance of point A [2,1] from the line p: X = -1 + 3 t Y = 5-4 t Line p has a parametric form of the line equation. - Water depth
 If the pool is 25 meters long and 10 meters wide and the water depth is 1.2 meters everywhere, how many square meters of the inside of the pool wet the water?
If the pool is 25 meters long and 10 meters wide and the water depth is 1.2 meters everywhere, how many square meters of the inside of the pool wet the water? - Nothing 4612
 How often can you take 5 euros from 30 euros until you have nothing left?
How often can you take 5 euros from 30 euros until you have nothing left? - Traveled journey
 The tourist traveled 3/8 of the planned journey on the first day and 7/12 of the trip on the second day. On which day did he travel most of the way, and by how much?
The tourist traveled 3/8 of the planned journey on the first day and 7/12 of the trip on the second day. On which day did he travel most of the way, and by how much? - A miner
 A miner is working at an elevation of -64 7/9 and then ascends 22 1/3. What is the miner's new location?
A miner is working at an elevation of -64 7/9 and then ascends 22 1/3. What is the miner's new location? - Increased 4120
 Which number increased by its seventh will give 32?
Which number increased by its seventh will give 32? - Distances 79974
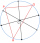 The picture shows three villages, A, B, and C, and their mutual air distances. The new straight railway line is to be built so that all the villages are the same distance from the line and that this distance is the smallest possible. How far will they be
The picture shows three villages, A, B, and C, and their mutual air distances. The new straight railway line is to be built so that all the villages are the same distance from the line and that this distance is the smallest possible. How far will they be - Hole's angles
 I am trying to find an angle. The top of the hole is .625", and the bottom of the hole is .532". The hole depth is .250". What is the angle of the hole (and what is the formula)?
I am trying to find an angle. The top of the hole is .625", and the bottom of the hole is .532". The hole depth is .250". What is the angle of the hole (and what is the formula)? - Frac equation v2
 3.80 is two-fifths of a quarter sum of money. How much money is there?
3.80 is two-fifths of a quarter sum of money. How much money is there? - Birthday
 The mother bought 21 desserts on the occasion of Mirka's birthday. One tip was 9 CZK, and the kremlin cost 12 CZK. For all desserts, she paid 213 CZK. How many kremlins and how many tips did mums buy?
The mother bought 21 desserts on the occasion of Mirka's birthday. One tip was 9 CZK, and the kremlin cost 12 CZK. For all desserts, she paid 213 CZK. How many kremlins and how many tips did mums buy? - The triangle 5
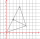 The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units?
The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units? - Two runners
 Two runners ran simultaneously towards each other from locations distant 23.1 km. The average speed of the first runner was 1/7 higher than the average speed of the second runner. How long should each run a 23.1 km, if you know they meet after 58 minutes?
Two runners ran simultaneously towards each other from locations distant 23.1 km. The average speed of the first runner was 1/7 higher than the average speed of the second runner. How long should each run a 23.1 km, if you know they meet after 58 minutes? - Solution 83019
 Kitchen vinegar is an 8% solution of acetic acid in water. How many liters of acetic acid are needed to produce 275 liters of vinegar?
Kitchen vinegar is an 8% solution of acetic acid in water. How many liters of acetic acid are needed to produce 275 liters of vinegar? - Calculate hexagon
 Calculate the area of a regular hexagon with side a = 2cm.
Calculate the area of a regular hexagon with side a = 2cm. - Calculate 5816
 A Boeing plane took off from the airport and flew at a speed of 900 km/h. When it had flown 600 km, a fighter plane was sent after it from the same airport, which flew at a speed of 2100 km/h. Calculate how long it took him to catch up.
A Boeing plane took off from the airport and flew at a speed of 900 km/h. When it had flown 600 km, a fighter plane was sent after it from the same airport, which flew at a speed of 2100 km/h. Calculate how long it took him to catch up.
more math problems »
