Lichoběžník MO
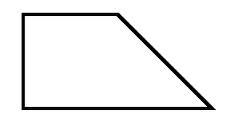
Je dán pravouhlý lichoběžník ABCD s pravým uhlem u bodu B, |AC| = 12, |CD| = 8, uhlopříčky jsou na sebe kolmé.
Vypočítejte obvod a obsah takéhoto lichobežníka.
Vypočítejte obvod a obsah takéhoto lichobežníka.
Správná odpověď:
Zobrazuji 3 komentáře:
Žák
mám za to, že cos(x)2+sin(x)2=1. Vy ale počítáte s tím, že 2cos(x)2=1. A to je asi blb2, ne?
4 roky 1 Like
Žák
Za předpokladu, že jsou zadány délky uhlopříček |AC| = 12 cm a |BD| = 8 cm je plocha příslušného pravoúhlého lichoběžníka 54 cm2 a obvod cca 30,5 cm.
Dr Math
Zadani neni jednoznacne, protoze dva vrcholy lichobeznika jsou s pravym uhlem, a tim neni jiste, ktery vrchol je bod B. Rovnez neni jasne orientace oznaceni vrcholu lichobeznika. Reseni prikladu by usnadnilo, kdyby v obrazku byly popsany vrcholy lichobeznika - A, B, C, D.
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- kvadratická rovnice
- rovnice
- aritmetika
- odmocnina
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- obsah
- obvod
- trojúhelník
- lichoběžník
- úhlopříčka
- základní funkce
- úvaha
- čísla
- zlomky
- goniometrie a trigonometrie
- sinus
- kosinus
- tangens
- arkustangens
- arkussinus
- arkuskosinus
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Čtyřúhelník
 Ukažte, že čtyřúhelník s vrcholy P1 (0,1), P2 (4,2) P3 (3,6) P4 (-5,4) má dva pravé trojúhelníky.
Ukažte, že čtyřúhelník s vrcholy P1 (0,1), P2 (4,2) P3 (3,6) P4 (-5,4) má dva pravé trojúhelníky. - Jak velká
 Jak velká je hnědě vybarvená plocha uvnitř čtverce o straně 6 cm, pokud každá ze čtyř hnědých kruhových úsečí je z kruhu o poloměru délky stany čtverce? Délka kruhových úsečí je rovna délce strany čtverce. Situace je vyobrazena na obrázku vpravo.
Jak velká je hnědě vybarvená plocha uvnitř čtverce o straně 6 cm, pokud každá ze čtyř hnědých kruhových úsečí je z kruhu o poloměru délky stany čtverce? Délka kruhových úsečí je rovna délce strany čtverce. Situace je vyobrazena na obrázku vpravo. - Vypočítejte 22
 Vypočítejte obsah kruhu, který má stejný obvod jako je obvod obdélníku vepsané kružnici o poloměru r 9 cm tak, že jeho strany jsou v poměru 2 ku 7.
Vypočítejte obsah kruhu, který má stejný obvod jako je obvod obdélníku vepsané kružnici o poloměru r 9 cm tak, že jeho strany jsou v poměru 2 ku 7. - Čtverci
 Čtverci o straně a=1 je vepsaná a opsaná kružnice. Určete obsah mezikruží.
Čtverci o straně a=1 je vepsaná a opsaná kružnice. Určete obsah mezikruží.
- Čtvrtkruh
 Jaký poloměr má kruh vepsaný do čtvrtkruhu o poloměru 100 cm?
Jaký poloměr má kruh vepsaný do čtvrtkruhu o poloměru 100 cm? - Valec naležato
 Válec o průměru 3m a výšce/délce 15 m je položen naležato. Je do něj napuštěna voda, která sahá do výšky 60 cm pod osu válce. Kolik hektolitrů vody je ve válci?
Válec o průměru 3m a výšce/délce 15 m je položen naležato. Je do něj napuštěna voda, která sahá do výšky 60 cm pod osu válce. Kolik hektolitrů vody je ve válci? - Rovnoběžníku 5027
 Vypočítejte obsah rovnoběžníku, pokud jsou velikosti stran a=80, b=60 a velikost úhlu sevřeného úhlopříčkami je 60°.
Vypočítejte obsah rovnoběžníku, pokud jsou velikosti stran a=80, b=60 a velikost úhlu sevřeného úhlopříčkami je 60°. - Úseč
 Vypočítejte plochu S úseče a délku kruhového oblouku l. Výška úseče je 2 cm a úhel α = 60°. Pomůcka: S = 1/2 r². (Β-sinβ)
Vypočítejte plochu S úseče a délku kruhového oblouku l. Výška úseče je 2 cm a úhel α = 60°. Pomůcka: S = 1/2 r². (Β-sinβ) - Mezikruží
 Čtverci o obsahu 16 centimetrů čtverečních je vepsaná kružnice k1 a opsána kružnice k2. Vypočtěte obsah mezikruží, které kružnice k1, k2 ohraničují.
Čtverci o obsahu 16 centimetrů čtverečních je vepsaná kružnice k1 a opsána kružnice k2. Vypočtěte obsah mezikruží, které kružnice k1, k2 ohraničují.
- Kruhový bazén
 Podstava bazénu má tvar kruhu o poloměru r = 10m kromě kruhového odstavce, který určuje tětiva délky 10m. Jeho hloubka je h = 2m. Kolik hektolitrů vody se vejde do bazénu?
Podstava bazénu má tvar kruhu o poloměru r = 10m kromě kruhového odstavce, který určuje tětiva délky 10m. Jeho hloubka je h = 2m. Kolik hektolitrů vody se vejde do bazénu? - Trojuhelníku 135
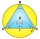 Trojuhelníku ABC o stranách a = 15 cm, b = 17,4 cm, c = 21,6 cm je opsána kružnice. Vypočítejte obsah úsečí určených stranami trojúhelníku.
Trojuhelníku ABC o stranách a = 15 cm, b = 17,4 cm, c = 21,6 cm je opsána kružnice. Vypočítejte obsah úsečí určených stranami trojúhelníku. - V trojúhelníku
 V trojúhelníku ABC vypočítejte velikosti všech výšek, úhlů, obvod a obsah, pokud je dané a-40cm, b-57cm, c-59cm
V trojúhelníku ABC vypočítejte velikosti všech výšek, úhlů, obvod a obsah, pokud je dané a-40cm, b-57cm, c-59cm - Obdélník úhlopříčka
 Vypočtěte obvod a obsah obdélníku, pokud jeho úhlopříčka má délku 14 cm a úhlopříčky svírají úhel 130°.
Vypočtěte obvod a obsah obdélníku, pokud jeho úhlopříčka má délku 14 cm a úhlopříčky svírají úhel 130°. - Plášť 8
 Plášť kužele je vytvořen svinutím kruhové úseče o poloměru 1. Pro jaký středový úhel dané kruhové výseče bude objem vzniklého kužele maximální?
Plášť kužele je vytvořen svinutím kruhové úseče o poloměru 1. Pro jaký středový úhel dané kruhové výseče bude objem vzniklého kužele maximální?
- V pravidelném 2
 V pravidelném čtyřbokem jehlanu je výška 6,5 cm a úhel mezi podstavou a boční stěnou je 42°. Vypočítej povrch a objem tělesa. Výpočty zaokrouhlit na 1 desetinné místo.
V pravidelném čtyřbokem jehlanu je výška 6,5 cm a úhel mezi podstavou a boční stěnou je 42°. Vypočítej povrch a objem tělesa. Výpočty zaokrouhlit na 1 desetinné místo. - Kosý hranol
 Jaký objem má čtyřboký kosý hranol s podstavnými hranami o délce a=1m, b=1,1m, c=1,2m, d=0,7m, jestliže boční hrana o délce h=3,9m má odchylku od podstavy 20°35´ a hrany a, b svírají úhel 50,5°.
Jaký objem má čtyřboký kosý hranol s podstavnými hranami o délce a=1m, b=1,1m, c=1,2m, d=0,7m, jestliže boční hrana o délce h=3,9m má odchylku od podstavy 20°35´ a hrany a, b svírají úhel 50,5°. - Lupínky - kvítek
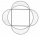 Čtvercu byl opsán kruh a nad každou stranou čtverce, jako nad průměrem, byl vyznačen půlkruh. Vznikly tak 4 lupínky. Co je větší: obsah středního čtverce, nebo obsah čtyř lupínků?
Čtvercu byl opsán kruh a nad každou stranou čtverce, jako nad průměrem, byl vyznačen půlkruh. Vznikly tak 4 lupínky. Co je větší: obsah středního čtverce, nebo obsah čtyř lupínků?
