Rovnobežník - uhlopriečky
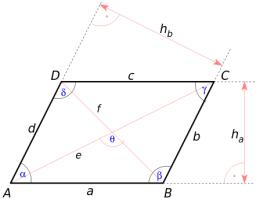
Vypočítajte obsah rovnobežníka, ak sú veľkosti strán a=80, b=60 a veľkosť uhla zovretého uhlopriečkami je 60°.
Správna odpoveď:
Zobrazujem 1 komentár:
Kristián
Vypočítajte obsah rovnobežníka so stranami a=25,3 b=13,8 a uhol zavretý stranami je a=72°
Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom koreňov kvadratickej rovnice?
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Štvoruholník
 Ukážte, že štvoruholník s vrcholmi P1 (0,1), P2 (4,2) P3 (3,6) P4 (-5,4) má dva pravé trojuholníky.
Ukážte, že štvoruholník s vrcholmi P1 (0,1), P2 (4,2) P3 (3,6) P4 (-5,4) má dva pravé trojuholníky. - Určte 9
 Určte vzdialenosť dvoch neprístupných miest P, Q, ak vzdialenosť dvoch pozorovacích miest A, B je 2000m a ak poznáte veľkosť uhlov QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažované miesta A, B, P, Q ležia v jednej rovine.
Určte vzdialenosť dvoch neprístupných miest P, Q, ak vzdialenosť dvoch pozorovacích miest A, B je 2000m a ak poznáte veľkosť uhlov QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažované miesta A, B, P, Q ležia v jednej rovine. - Obsah kruhu
 Vypočítajte obsah kruhu, ktorý má rovnaký obvod ako je obvod obdĺžnika vpísanej kružnici s polomerom r 9 cm tak, že jeho strany sú v pomere 2 ku 7.
Vypočítajte obsah kruhu, ktorý má rovnaký obvod ako je obvod obdĺžnika vpísanej kružnici s polomerom r 9 cm tak, že jeho strany sú v pomere 2 ku 7. - Medzikružie
 Štvorcu o strane a = 1 je vpísaná a opísaná kružnica. Určte obsah medzikružia.
Štvorcu o strane a = 1 je vpísaná a opísaná kružnica. Určte obsah medzikružia.
- Štvrťkruh 4
 Aký polomer má kruh vpisany do štvrťkruhu s polomerom 100 cm?
Aký polomer má kruh vpisany do štvrťkruhu s polomerom 100 cm? - Valec naležato
 Valec s priemerom 3m a výškou/dĺžkou 15 m je položený naležato. Je doň napustená voda, ktorá siaha do výšky 60 cm pod os valca. Koľko hektolitrov vody je vo valci?
Valec s priemerom 3m a výškou/dĺžkou 15 m je položený naležato. Je doň napustená voda, ktorá siaha do výšky 60 cm pod os valca. Koľko hektolitrov vody je vo valci? - Odsek a oblúk
 Vypočítaj plochu S odseku a dľžku kružnicového oblúka l . Výška odseku je 2 cm a uhol α=60°. Pomôcka: S=1/2 r² . (β-sinβ)
Vypočítaj plochu S odseku a dľžku kružnicového oblúka l . Výška odseku je 2 cm a uhol α=60°. Pomôcka: S=1/2 r² . (β-sinβ) - Medzikružie
 Štvorcu o obsahu 16 centimetrov štvorcových je vpísaná kružnica k1 a opísaná kružnica k2. Vypočítajte obsah medzikružia, ktoré kružnice k1, k2 ohraničujú.
Štvorcu o obsahu 16 centimetrov štvorcových je vpísaná kružnica k1 a opísaná kružnica k2. Vypočítajte obsah medzikružia, ktoré kružnice k1, k2 ohraničujú. - Kruhový bazén
 Podstava bazéna má tvar kruhu s polomerom r=10m okrem kruhového odseku, ktorý určuje tetiva dĺžky 10m. Jeho hĺbka je h=2m. Koľko hektolitrov vody sa zmesti do bazéna?
Podstava bazéna má tvar kruhu s polomerom r=10m okrem kruhového odseku, ktorý určuje tetiva dĺžky 10m. Jeho hĺbka je h=2m. Koľko hektolitrov vody sa zmesti do bazéna?
- V trojuholníku 18
 V trojuholníku ABC je dané b=5 cm, c=6 cm, /BAC/ = 80°. Vypočítajte veľkosti ostatných strán a uhlov, ďalej určte veľkosti ťažnice tc a obsah trojuholníka.
V trojuholníku ABC je dané b=5 cm, c=6 cm, /BAC/ = 80°. Vypočítajte veľkosti ostatných strán a uhlov, ďalej určte veľkosti ťažnice tc a obsah trojuholníka. - V trojuholníku 10
 V trojuholníku ABC vypočítajte veľkosti všetkých výšok, uhlov, obvod a obsah, ak je dané a-40cm, b-57cm, c-59cm
V trojuholníku ABC vypočítajte veľkosti všetkých výšok, uhlov, obvod a obsah, ak je dané a-40cm, b-57cm, c-59cm - Vypočítajte 52
 Vypočítajte obvod a obsah obdĺžnika, ak jeho uhlopriečka má dĺžku 14 cm a uhlopriečky zvierajú uhol 130°.
Vypočítajte obvod a obsah obdĺžnika, ak jeho uhlopriečka má dĺžku 14 cm a uhlopriečky zvierajú uhol 130°. - Plášť
 Plášť kužeľa je vytvorený zvinutím kruhového výseku s polomerom 1. Pre aký stredový uhol daného kruhového výseku bude objem vzniknutého kužeľa maximálnu?
Plášť kužeľa je vytvorený zvinutím kruhového výseku s polomerom 1. Pre aký stredový uhol daného kruhového výseku bude objem vzniknutého kužeľa maximálnu? - Štvorboký ihlan - objem a povrch
 V pravidelnom štvorbokom ihlane je výška 6,5 cm a uhol medzi podstavou a bočnou stenou je 42°. Vypočítaj povrch a objem telesa. Výpočty zaokrúhliť na 1 desatinné miesto.
V pravidelnom štvorbokom ihlane je výška 6,5 cm a uhol medzi podstavou a bočnou stenou je 42°. Vypočítaj povrch a objem telesa. Výpočty zaokrúhliť na 1 desatinné miesto.
- Kosý hranol
 Aký objem má štvorboký kosý hranol s podstavnými hranami o dĺžke a = 1m, b = 1,1m, c = 1,2 m, d = 0,7m, ak bočná hrana s dĺžkou h = 3,9m má odchýlku od podstavy 20° 35 'a hrany a, b zvierajú uhol 50,5°.
Aký objem má štvorboký kosý hranol s podstavnými hranami o dĺžke a = 1m, b = 1,1m, c = 1,2 m, d = 0,7m, ak bočná hrana s dĺžkou h = 3,9m má odchýlku od podstavy 20° 35 'a hrany a, b zvierajú uhol 50,5°. - Kvietok
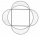 Štvorcu bol opísaný kruh a nad každou stranou štvorca, ako nad priemerom, bol vyznačený polkruh. Vznikli tak 4 lupienky. Čo je väčšie: obsah stredného štvorca, alebo obsah štyroch lupienkov?
Štvorcu bol opísaný kruh a nad každou stranou štvorca, ako nad priemerom, bol vyznačený polkruh. Vznikli tak 4 lupienky. Čo je väčšie: obsah stredného štvorca, alebo obsah štyroch lupienkov? - Dekanon
 Vypočítajte obvod a obsah pravidelného 10 uholníka ak polomer opísanej kružnice r = 20 cm.
Vypočítajte obvod a obsah pravidelného 10 uholníka ak polomer opísanej kružnice r = 20 cm.
